The area rule states that the area of any triangle is equal to half the product of the lengths of the two sides of the triangle multiplied by the sine.
Area Of Triangle Formula Sine Rule. Here are a number of highest rated area triangle sine pictures on internet. Sin sin sin ab c a bc.
Sine Rule for the Area of a Triangle YouTube From youtube.com
Remember that the given angle must be between the two given sides. The two attached word documents are two versions of a match up type activity. (\text {area}) = \frac {1} {2} ch.
Sine Rule for the Area of a Triangle YouTube
Area = ½ ab sin c. ©mathsdly.com page 5 of 9. The sine rule and cosine rule are formulas that can be used to assist you in finding the unknown side or angle of a triangle when given enough information. Sine rule the sine rule connects the length of sides and angles in any triangle abc:
Source: slideshare.net
The height is b × sin a. Area = (1 / 2) b c sin(a) = (1 / 2) c a sin(b) = (1 / 2) a b sin(c) how to use the calculator here we assume that we are given sides a and b and the angle between them c. For example, consider the triangle pqr below: We know.
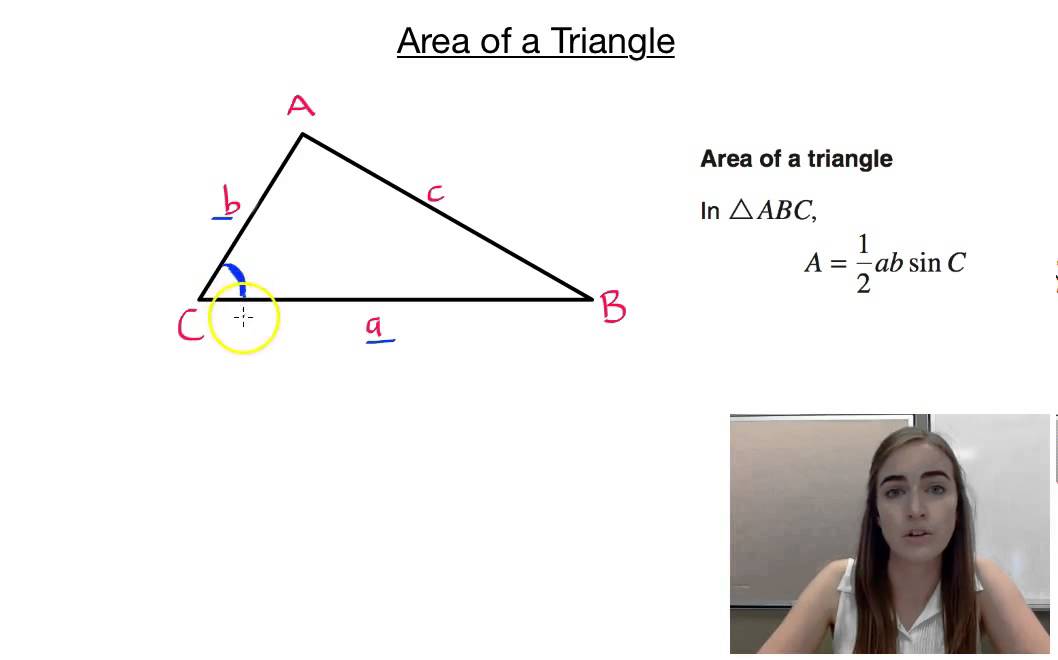Source: youtube.com
Area = ½ × base × height. (\text {area}) = \frac {1} {2} ch. Area = ½ × (c) × (b × sin a) which can be simplified to: Sine rule (the law of sine): ( area) = 1 2 c h.
Source: youtube.com
The area of a triangle using sine. Similarly, by constructing a perpendicular height from vertex b b to the line ac a c, we can also show that area abc = 1 2 bcsin ^a a b c = 1 2 b c sin. The area of any triangle can be calculated using the formula: Area = ½ × (c).
Source: youtube.com
The area of any triangle can be calculated using the formula: Sina a = sinb b = sinc c. ( area) = 1 2 c h. The sine rule and cosine rule are formulas that can be used to assist you in finding the unknown side or angle of a triangle when given enough information. It allows us to find.
Source: aplustopper.com
Area = ½ × (c) × (b × sin a) which can be simplified to: Cosine rule (the law of cosine): A triangle doesn’t have to be labelled using the letters a, b and c. If your calculator gives you a ‘maths error’ message when trying to find an angle using the cosine rule, you probably subtracted things the wrong.
Source: youtube.com
An alternative version of the formula is often used when finding the size of angles: Area of abc = 1 2absinc. Area = (1 / 2) b c sin(a) = (1 / 2) c a sin(b) = (1 / 2) a b sin(c) how to use the calculator here we assume that we are given sides a and b and.
