With two separate triangles, one with 30 and 60 degrees and the other with 45 and 90 degrees, be prepared for every situation with these drafting triangles. If the longer.
30 60 90 Triangle 45 45 90. Of all these special right triangles, the two encountered most often are the 30 60 90 and the 45 45 90 triangles. The 45 45 90 triangle calculator shows the remaining parameters.
Better Questions Special Right Triangles Mrs. Newell�s Math From newellssecondarymath.blogspot.com
Special triangles in geometry because of the powerful relationships that unfold when studying their angles and sides. Another rule is that the two sides of the triangle or legs of the triangle that form the right angle. For hypotenuse c known, the legs formulas look as follows:
Better Questions Special Right Triangles Mrs. Newell�s Math
Multiply that leg by 2. Special triangles in geometry because of the powerful relationships that unfold when studying their angles and sides. Leave your answers as radicals in simplest form. Multiply that leg by 2.
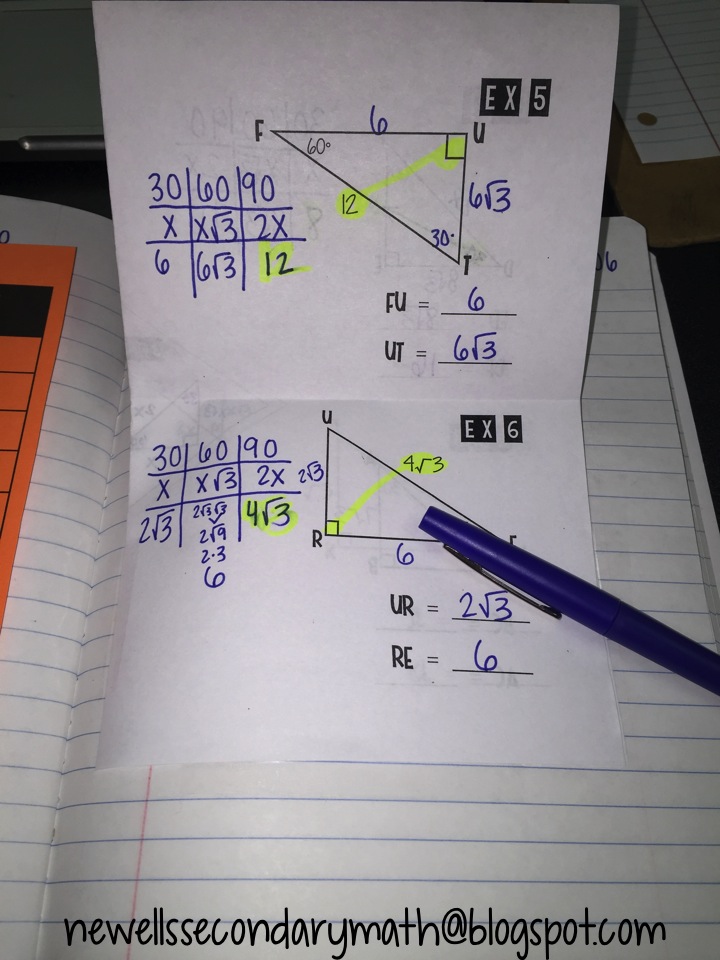Source: newellssecondarymath.blogspot.com
Because it is a special triangle, it also has side length values which are always in a consistent relationship with one another. For hypotenuse c known, the legs formulas look as follows: Use the same length for the second leg. If the longer leg length b is the one parameter given, then: Special triangles in geometry because of the powerful.
Source: ambiance-sticker.com
Of all these special right triangles, the two encountered most often are the 30 60 90 and the 45 45 90 triangles. Multiply that leg by √2. This is an isosceles right triangle. For hypotenuse c known, the legs formulas look as follows: It has two acute angles and one right angle.
Source: petrofilm.com
For example, a speed square used by carpenters is a 45 45 90 triangle. If the longer leg length b is the one parameter given, then: For example, in the triangle below at left, 55q 40q 85q 180q. In a triangle whose angles measure 30 0, 60 0, and 90 , the hypotenuse has a length 0 equal to twice.
Source: atwood202.blogspot.com
If the longer leg length b is the one parameter given, then: For example, in the triangle below at left, 55q 40q 85q 180q. If we know the shorter leg length a, we can find out that: Use the same length for the second leg. Multiply that leg by √2.
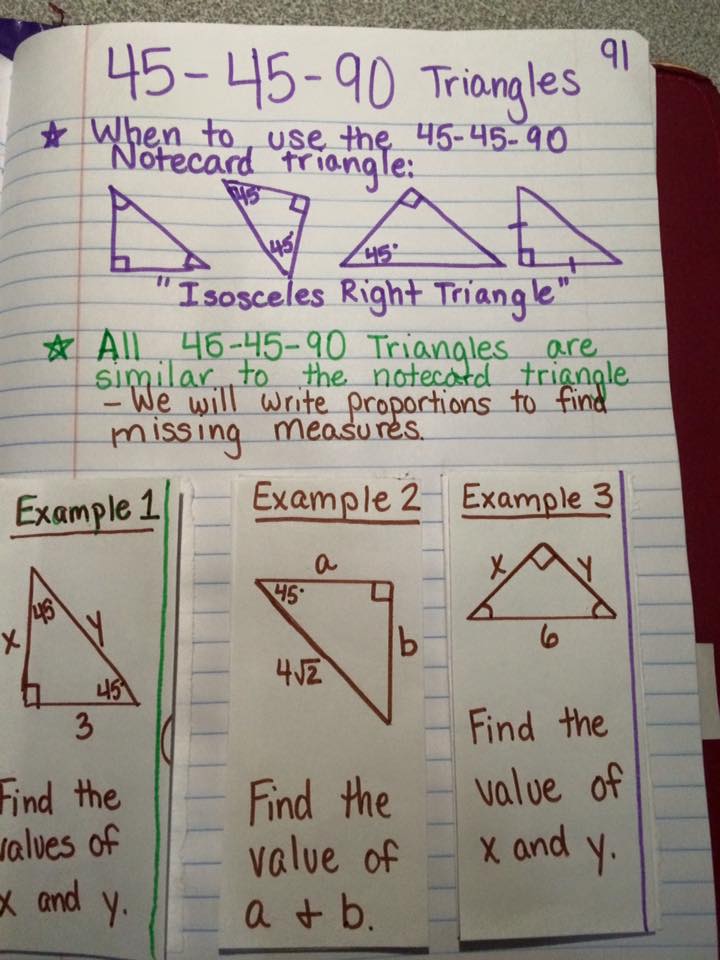Source: atwood202.blogspot.com
If we know the shorter leg length a, we can find out that: For hypotenuse c known, the legs formulas look as follows: If the longer leg length b is the one parameter given, then: In the day before computers when people actually had to draw angles, special tools called drawing triangles were used and the two most popular were.
Source: wall.alphacoders.com
Use the same length for the second leg. Both are right angle triangles the square of the hypotenuse equals the sum of the squares of the other two sides for both triangles both triangles lie entirely in a plane (mot necessarily the same plane) both are not acute triangles both are not obtuse triangle. 30 60 90 triangle 45 45.
